今回は円周振れと全振れについてです。振れ公差は幾何公差の中でも測定方法がわかりやすいので、多用したいところですが、活躍の場が限定されます。また、考え方として絶対理解しておきたい同軸度(同心度)との関係性がありますので、解説していきます。
円周振れとは
円周振れとは、データムを基準にして回転させたとき、指定された点がどれだけ振れても良いか、を示します。ダイヤルゲージを当てたら動かしません。
全振れとは
全振れとは、データムを基準にして回転させたとき、指定された範囲がどれだけ振れても良いか、を示します。ダイヤルゲージを指定の範囲すべてをカバーするように動かします。
円周振れ=全振れとは限らない
両方ともデータムを基準に回転させたところへダイヤルゲージを当てるので、一見同じように見えますが、上でも触れた通り、動かすか、動かさないかの違いがあります。これにより、測定値が違う場合があります。下の絵を見てください。
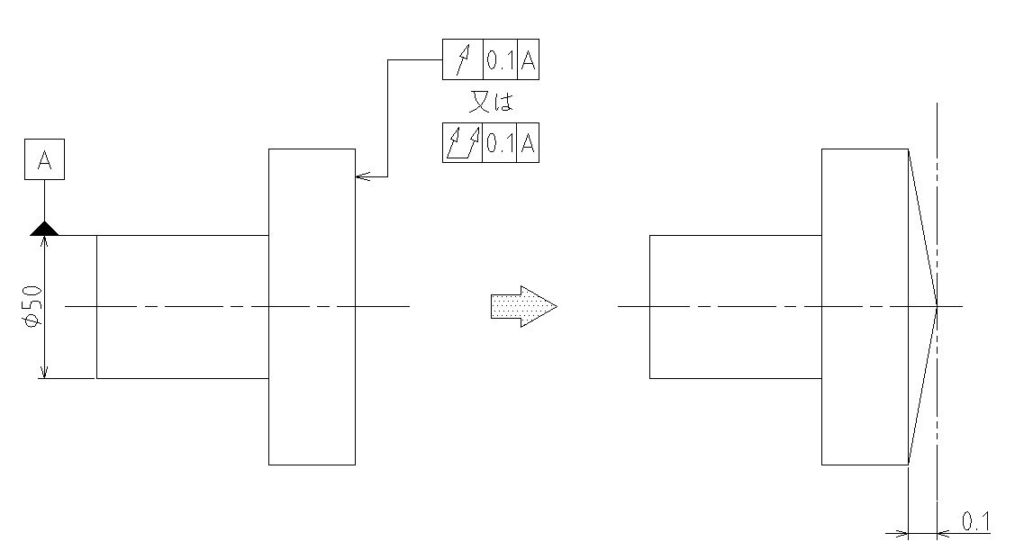
左のような図面で右のような部品が出来上がったとします。右側の端面が円錐状に0.1だけ凸になってしまった場合です。
幾何公差が円周振れ(上)の場合、実際にできた部分が円錐状になっているだけであれば、ダイヤルゲージを動かしませんので、測定値は0になります。
ところが、幾何公差が全振れ(下)の場合、指定された面全てにダイヤルゲージを動かしながら測定しますので、測定結果は0.1となります。
寸法線からは明確に外す
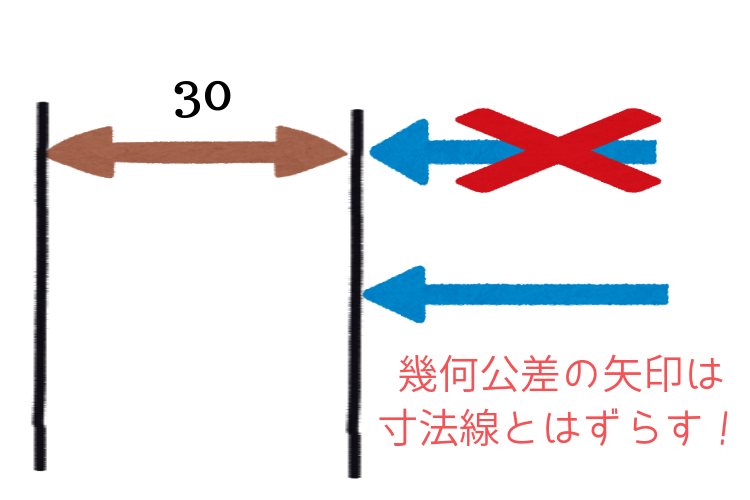
円周振れと全振れを示す場合、寸法線から明確にずれた位置で指示します。
明確に外す=指定された場所の表面 ですから、回転させた表面を測定する円周振れと全振れは明確に外します。
寸法線と重なる位置に円周振れまたは全振れの指示が合った場合は間違いです!
データムは必ず必要 Φは不要
円周振れ、全振れ、両方とも回転させたときのダイヤルゲージの値を読み取るため、回転させるための基準、つまりデータムが必ず必要です。
また、測定値はダイヤルゲージの変化量となり、範囲は幅を示すので、許容範囲にΦを記載する必要はありません。言い換えると、ついていると恥ずかしいのでやめましょう。
検証方法
この、振れ系の幾何公差は測定結果がそのまま検証結果です!幾何公差の中で最もわかりやすいのではないでしょうか?
振れとオフセット量の関係は理解しておくと良い

振れの半分がオフセット量=(ほぼ)同心度
円周振れや全振れの測定と同じ方法で同心度を検証する場合があります。この時注意したいのが、同心度は振れの半分になるというところです。
半径が50 mm の円を考えます。
その円の中心から1 mm だけずれた(オフセットした)位置を中心にして円を回転させてた場合、円の外周の移動量=ダイヤルゲージの読み値(振れ)を考えると、その値は2 mmになります。回転するたびに、決まった点は1 mm増えたり減ったりしますからね。
オフセット量は振れの半分と覚えておくと良いと思います。
オフセットしているとみなせるのは、ダイヤルゲージの最大値と最小値が正反対になった時のみ
単純にダイヤルゲージの最大値と最小値の差の半分がオフセット量と考えるのはよくありません。
そう考えることができるのは、最大値と最小値がリニアに(なめらかに)変化し、かつ最大値と最小値が正反対の場所に現れるときだけです。つまり、真円度が担保されている時だけです。
円を測定していて、例えば一か所だけごみがついていて異常に膨らんでいたりすると、振れの半分がオフセット量にはなりませんよね。
まとめ
円周振れ、全振れは回転体にしか使えない!
他の幾何公差の検証に使えるけど、振れとオフセット量の違いに注意!


コメント