幾何公差シリーズ。今回は普通幾何公差に焦点を当ててみます。
先日、こんなアンケートを取りました。

投票いただいた方ありがとうございました!
現在普通幾何公差の導入を考えていまして、色々調べた結果をまとめて紹介していきたいと思います。
- 普通幾何公差とは何かざっくり知りたい人
- 思わぬメリット・デメリットを知りたい人
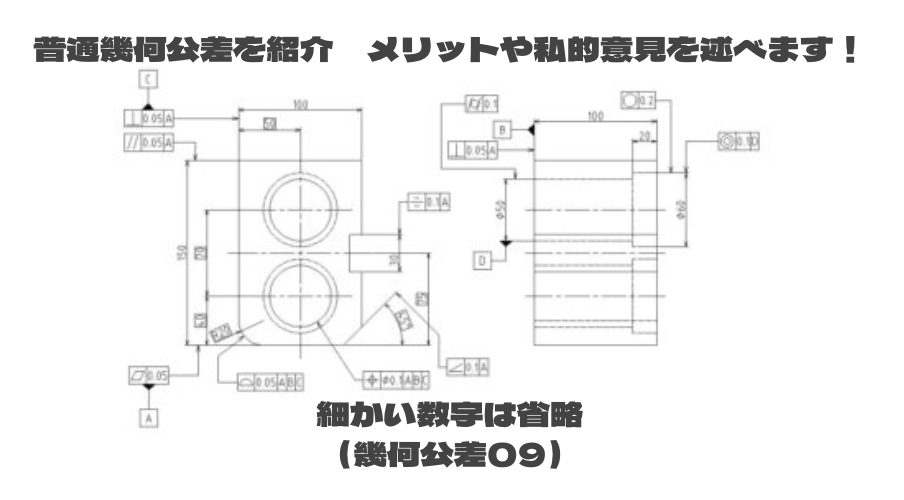
ざっくりいうと指示なき加工面の幾何公差を指定します
詳しいことはJIS B 0419に書いてありますので、省略します。
注目は「加工面」であるということ。鋳肌や黒皮には当てはめられません。
考え方は削り加工の一般公差と一緒なんですね!
ちなみに鋳物関係の幾何公差はあまり聞きませんが、JIS B 0403−1995で色々規定がされていますので、参考にしてみてください。
鋳物に関してはこちらにダラダラとまとめてありますので、ご興味があれば是非・・・。
普通幾何公差の規定がない幾何公差もあります
普通幾何公差が規定されていない幾何公差もあるんです。円筒度、線の(面の)輪郭度、傾斜度、同軸度、位置度、全振れは普通幾何公差の規定がありません。
裏を返すと、これらの幾何公差を指定したければ個々に指示する必要があるということです。難しい特別な幾何公差だと考えておいた方がいいでしょう。
このようなことは規格を読むことでわかります。
話の本筋からは逸れますが、規格を読むというのは参考書の勉強とはまた違った理解を得ることができるのでおすすめですよ!
規格から学べることは多いです。機械設計者の皆様、教わらなかったことは常識だそうです。
メリット紹介 思わぬメリットあります
機械加工をする工場の品質向上
普通幾何公差はとても緩い公差であるにもかかわらず工場の品質が向上する可能性があります。なぜなのでしょうか?
普通幾何公差を規定するということは、あまり気を使わなくて良い加工にゆるーい精度縛りができる、という感じです。
一歩踏み込んで考えると、何気ない加工に対して、少なくとも精度の縛りをクリアできる加工能力が必要であると言えます。
この加工能力を担保するために、普段から抜き取り検査などを実行する必要があります。定期的に検査をしてチェックしなければ、決められている普通幾何公差をクリアしているとは言えませんよね。
よって工場の品質が定期的にチェックされる、という意味で品質向上の効果があると言えます。
幾何公差の「普通」の統一化ができる
個人的に結構良いなぁと思うことは、幾何公差の「普通」という概念が設計者、加工者、検査者等、ものづくりの一連の関係者で統一できるという点です。
意外と「普通」って各個人で違っちゃっていますから。。。
普通を定義してしまえるので「普通でいいって思ってたのに、思ってたんとちゃう!」ということがありません。
製図時時短による効率化(手抜きできる)
これは設計者にとってのメリットになりますが、余計な幾何公差を書かずに済みます。普通で良いところは普通でいいですからね。
余計な幾何公差を書かなくて済むので、図面が見やすくなります。図面が見やすい=加工ミスが減るということですので、これも品質向上の一つになるのではないでしょうか。
致命的でなければ公差外でもいいんです
実はこの規格で規制された幾何公差は外れてもいい場合があります。普通幾何公差は目安的な扱いなんです。規格本文から引用します。
機能によって許容される公差は,普通公差よりも大きいことがしばしばある。そのため,工作物のいずれかの形体で普通公差を(ときおり)超えても,部品の機能が必ずしも損なわれるとは限らない。普通公差から逸脱し,機能を損なう時だけ,その工作物を不採用にする。
JIS B 0419-1991 より引用
つまり製品に影響がなければ多少外れてても大丈夫というのが規格で決まっています。
どうでもいいところがちょっと外れただけで不採用になるケースを救済できるのでいいと思います。
良くも悪くも日本人らしいですね。。。でも実はこれは元々ISOなので海外規格なのですが・・・w
導入時に注意すること(デメリット)

おお、普通幾何公差いいね!早速導入じゃ!

いえいえ、待ってください。今弊社もここでストップ中です。落とし穴もあるので導入する際は注意が必要ですよ!いくつか注意しておきたい点をまとめておきます。
製造工場との打ち合わせ必要です 思わぬコストアップも
ここまで、工場の精度が向上したり、図面がすっきりしたり、いいことばかり書いてきましたが、場合によってはコストアップする場合があります。
それは打ち合わせをせずにいきなり図面に「JIS B 0419 普通幾何公差〇級による」と記入した場合です。
普通幾何公差を知らない人からすれば「訳のわからない制約がついただけ」となり、「余計な注意をしないといけないのでコストアップです!」と言われてしまうでしょう。
工場も混乱してしまうはずです。
導入する時は目的と理由を丁寧に説明することが必要ですね!
文句は言えません
先ほどは「普通幾何公差はゆるーい縛りがつく」と述べましたが、じつは縛りはありません。
「検査で普通幾何公差から外れていたとしても、機能を損なう場合のみ不合格とする」という記述が規格内にありましたよね。
ゆるーい縛りでもズレてほしくない場所は普通幾何公差の範囲であっても幾何公差を記入すべきでしょう。
サトー的には導入すべきと考えます!
メリットばかりではない普通幾何公差ですが、サトー的には導入すべきと考えます。
図面上で不明瞭な箇所は避けるべき
日本人のいいところである以心伝心。最近はあまり認められなくなりました。図面に書いてなくても、これはこう加工するのが常識でしょ!みたいなことが許されず、どんどん厳密さが増していきます。
かといって細かく記入しすぎると図面は見難いです。
厳密さが増している中で、一部の寸法を省略できる普通幾何公差は今の製図環境にとてもマッチしていると思います。
わかりやすい図面を書くことにつながる
図面を突き詰めて書いていくと、その図面については結局自分が一番わかるし、相手に100%わかってもらうことはできないということに気づきます。
それでも、相手の理解度を100%に近づける最大限の努力はすべきです。
かといって、近づける努力をして、あまり意味のない幾何公差を図面に描きまくると、かえって図面が見辛くなって理解度が下がる原因にもなってしまいます。本末転倒です。
図面を簡略化できる普通幾何公差は「手抜き」であると同時に、ゴチャゴチャしやすい幾何公差を簡略化することによって、わかりやすい図面を書くことができる「作業改善」にも繋がっています。
まとめ
普通幾何公差を理解・導入してみませんか?
工場にとっても、設計者にとってもメリットは大きいですよ!



コメント